どうも、婚活戦士イモリです。
もう、だいぶ前になるんですがNHKのスーパープレゼンテーションという番組で「数学による愛の必勝法」なるものをやっていたので紹介します。
番組自体は伊藤穣一とスプツニ子がTEDの面白いやつを紹介してコメントするっていう30分程度のシンプルなモノ。
打ち切りになってしまったものの、教養にもなるし、副音声は英語学習に最適、非常に興味深いものでした。
本題に入りますが、「数学による愛の必勝法」にて紹介していたものは「最適停止理論」というもの。
Wikipedia には「秘書問題」として紹介されており、また、「37%の法則」とも言うそう。
以下は、最適なパートナーを見つけるという課題に対する、前提条件と結論です。
前提条件:パートナーの選定方法を、総計n人のパートナーから順に検討していくものとする。現在、検討中のパートナー候補をr番目の候補者とし、最適なパートナーと見なすかの判定を、これまでに出会ったパートナー候補r-1人と比較して最も相応しいか、否か、を基準とする。
Ex) 既に5人のパートナー候補と出会った上に、6人目のパートナー候補者と会って検討をしている。今までの5人に比べて6人目の人物がより良いと思った場合、6人目は最適のパートナーと見なし、また、以前の5人の誰かに劣ると考えた場合、6人目は最適のパートナーと見なさない。
結論:人生でn人のパートナー候補と出会うと想定したとき、r番目の候補者が最適のパートナーである確率P(r)は下記に示される。(i≧2, r≧2)
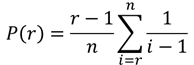
そしてこの式を解いたもの(2≦r≦n≦10)が以下の表
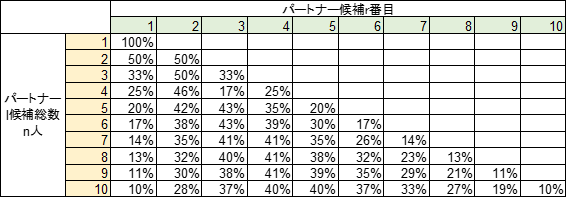
この解は非常に興味深いと思いませんか?
パートナーに合っていくにつれて、最適なパートナーに合う確率は徐々に上がり、また、途中から徐々に下がっていく。
種明かしをすると、P(r)は下記の式に近似変換される。
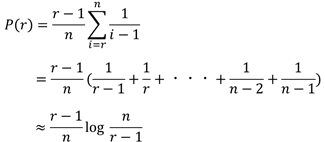
(ただし、近似においてnはある程度大きい数である必要がある)
改めて近似値をP’(r)として定義すると
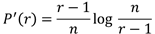
極大値を求めるためにrで微分して
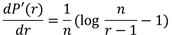
極大値の条件は下記になる。
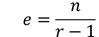
極大値を取る条件を元のP(r)に代入してみよう(言い換えると最適なパートナーが見つかる可能性が最も高いタイミングを見出しましょう。)
代入すると式はかなりすっきりして、
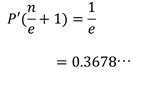
また、nを十分に大きい値にして横軸r、縦軸をP’(r)とすると、下図の関数が得られる。
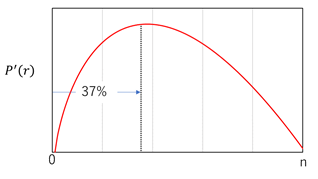
P(r)の極大がnに対してrがおよそ37%の時点で迎えることが、37%の法則と呼ばれる所以である。
この結果の最も知られている解釈は、
- 最適なパートナーが見つかる可能性が最も高い手法は、パートナー候補の内、最初のうち30%くらいは相手をせず、将来の比較対象としてのみに考える。37%あたりになって出会ったr番目のパートナー候補が今までにあったr-1人より、良いパートナー候補である、と思えば、その人が最適なパートナーである確率が最も高くなる、ということである。
もし、仮に20-35歳をパートナー探しの適齢期として、毎年1人のパートナー候補に出会うとすれば、合計で出会うパートナー候補は16人。最初の30%にあたる最初数人のパートナー候補は最良のパートナーである確率が低く、26歳近傍で出会ったパートナー候補が今までの候補者より良ければ、その人が“運命の人”に相当する確率が最大となる。
最適停止理論に基づく、恋愛指針は非常に分かりやすく、非常に実践しやすい指針とも言えよう。前半の恋愛は前哨戦程度と考えて適当に流して、中盤辺りから真面目に取り組む。中盤戦に差し掛かるころに素晴らしい人を見つけ、終盤に突入することなくコールド勝ちする(素敵なパートナーと結ばれる)という指針である。
しかしながら、この式は、いくつかのリスクを孕んでいる。
①冒頭に最適のパートナーがいた場合
「37%の法則」においては、最初の30数%に素敵だと思う人がいたとしても、その相手が最適なパートナーである確率は低いため、今後の判断材料のみとしてしか考えず、その次のパートナー候補を探した方が効率的だと言っている。しかし、言い換えると、最初の30数%で出会った人の中で、運命の相手とも言えうるような最適のパートナーの人がいた場合、以降は、現れもしない運命の相手の幻想を抱きながら、寂しい一生を終えることになる。
運命の相手と呼べるような最適なパートナーを見つけるのであれば、結局、序盤の吟味も十分に必要である。最適停止理論は有益だが、決して必勝法とは言えないし、妄信してはならない。
②P’(r)はnによって大きな影響を受けること
P’(r)は多くの人をパートナー候補として検討することを前提とした場合に、それなりの精度が出る式である。nが小さければ、P’(r)は乱高下するため、式はあまり当てにならない。
また、rがnに対する37%である際にP’(r)は最大値を取るが、P’(r)自体の値は変化する。
パートナー候補者総数nがより大きくなれば、当然、その中で巡り合ったパートナー候補が最適な相手である確率P’(r)は反比例して下がる。そういった意味では、マッチングアプリやお見合いで徒にパートナー候補者総数nを稼ぐことは賢明でない。極論、nが1であれば、必然的にその人が最適なパートナーであるし、ある意味、本当の意味での必勝法であると言えよう。極論、一途しか勝たん。
③自分が最適のパートナーを見つける確率を論じた式に過ぎないこと
P’(r)では自分の中での相対評価(順位付け)を最適な形で表す式として用いられるが、その一方、相手からどう思われるか、つまり、そもそも恋愛が成就するかというファクターが考慮されていない。パートナー関係の成立に関して当式の守備範囲外となる。
④あくまでも相対評価であること
パートナー候補を、主観に基づいて評価をする。もちろん、人の趣向・評価基準は変動するし、”好き”の定量評価は困難。最悪の場合、趣向の変動によって、最適なパートナーを見出し損ねる恐れがある。また、①とも関連するが、初恋の相手や昔の結実しなかった恋が懐古されてしまっている場合は、なおタチが悪い。
⑤37%以降は右下がりであるということ
P’(r)は37%という固有値を最大値として、以降は一様に減少する。さらに、その下降幅は年々大きくなる。これは、まさに婚期を逃すと良いパートナーに巡り合えないことを裏付ける一つの数学的な根拠と言えよう。日本の平均初婚年齢はざっと、夫 31 歳、妻 29歳、そして初婚までの平均交際期間は約4年だそうだ。結婚を焦点にあてた場合、26歳近傍が勝負になると解釈するのが妥当。(自分が書いた文から猛烈にプレッシャーを感じる。。。)
以上、最適なパートナーと巡り合うための指針を、数式を基に示し、検証を行った。今回は恋愛についてしか応用をしていないが、就活、家選び、賭け事の際に「37%の法則」は実践したい。




コメント